
PID controller – definition, operating principle, setting, and application areas
PID controllers are used to influence certain measurands. As clever 3-in-1 controllers, they prove themselves every day in numerous industrial systems and control very precisely up to the setpoint value. We provide you with the most important facts and figures about the PID regulation.
Table of contents
What is a PID controller?
A compact controller can be adapted to a wide variety of applications and is usually used as a PID controller. It operates in a manner that is proportional, integrating, and differentiating (PID). Here the intensity of the individual components is adapted to the control process. This is done via the dimensioning of the control parameters
- Pb (proportional band),
- rt (reset time), and
- dt (derivative time).
How do PID controllers work?
The principle of a PID controller is relatively simple to explain. No matter whether the controller is a PID temperature controller or a PID humidity controller, the controller always attempts to adjust a specific control variable to the setpoint value based on the actual value. In this case, the P component amplifies the control deviation, the I component increases its output level in case of existing control deviation, and the D component counteracts the movement of the actual value. Components that are not required for control can be deactivated. Depending on the application, they are then operated as PI controllers, P controllers, PD controllers, or I controllers.
In which applications are PID controllers used?
The PID structure demonstrates the best control response for the majority of applications. As a result, PID compact controllers are very common in the field of temperature control. They also allow a direct connection of RTD temperature probes and thermocouples. Some controlled variables require certain components to be disabled, including speed and flow.
What is behind the PID components and the respective control parameters?
The P component reacts very quickly and amplifies the control difference; its permanent control deviation has a disadvantageous effect. The responsible control parameter is the proportional band Pb. With smaller dimensioned Pb the controller becomes faster and the control deviation smaller. However, the overall system tends to oscillate more and more.
The I component eliminates the control deviation. If the reset time rt is set smaller, the controller builds up its output level faster and also counteracts the control deviation faster. However, if the setting is too small, oscillatory behavior will also occur.
The D component counteracts the movement of the actual value. This means for a heating controller that the component is reduced when the actual value increases and is increased when the actual value decreases. The described behavior has a dampening effect. The responsible parameter is the derivative time dt. The larger dt is set, the greater the described effect.
How are PID controllers optimized?
The behavior of the control process always depends on the working point. Before tuning, the plant must therefore be set to an operating status for which favorable control parameters are expected later on. For example, a furnace should be loaded before tuning, or a demand must be generated for a flow heater. If a setpoint value needs to be specified during tuning, this should lie within the subsequent working range.
If comparable plants/control loops exist, the control parameters used in them can be used on a trial basis. If this approach does not lead to the goal, one of the following optimization methods can be used.
The oscillation method according to Ziegler and Nichols
This method is used for relatively fast controlled systems. To prepare, the P structure is parameterized and a relatively large Pb is set. A setpoint value lying within the subsequent working range is defined in the following figure.
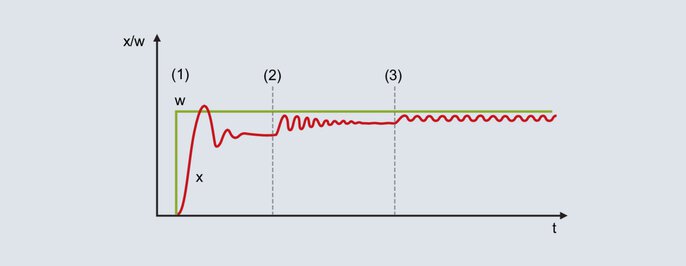
Fig. 52: Setpoint and actual value curve when using the oscillation method
With the proportional band set relatively large, the actual value moves to the end value with little tendency to oscillation [Figure 52 (1)]. Due to the non-existent I structure a permanent control deviation is present.
The Pb is reduced (Figure 52 [2]): the actual value increases and moves to the end value with a greater tendency to oscillation. In certain circumstances the proportional band is reduced several times until the actual value is permanently oscillating (Figure 52 [3]). The proportional band required for this behavior is called Pbc (critical Pb) and must be determined as accurately as possible (do not reduce Pb in excessively large steps).
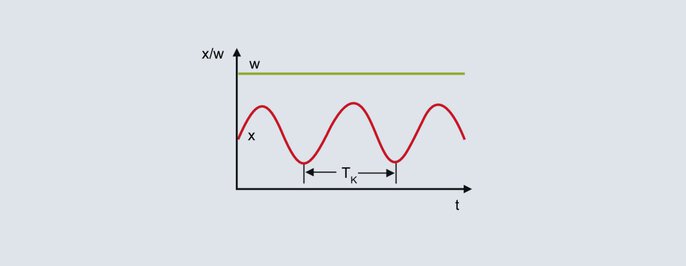
Critical period
From the continuous oscillation of the actual value in the upper figure, the critical period duration Tc represents the second characterizing parameter to be determined for the method. The critical period duration Tc (in seconds) is calculated from the time interval between 2 minimum values, for example. To determine the control parameters, Pbc and Tc are inserted into the following table for the intended controller structure:
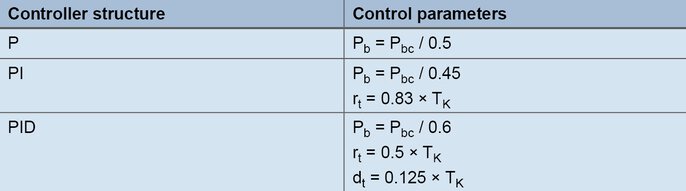
Formulas for setting according to the oscillation method
Method on the basis of the process step response according to Chien, Hrones, and Reswick
With this method the control parameters are calculated relatively quickly, even for slow control processes. The method is applied for processes as from the second order and is characterized by the fact that it distinguishes between the formulas for transient behavior and disturbance behavior. For the rules of thumb, the transfer coefficient of the control process, the delay time, and the compensation time are calculated on the basis of the step response.
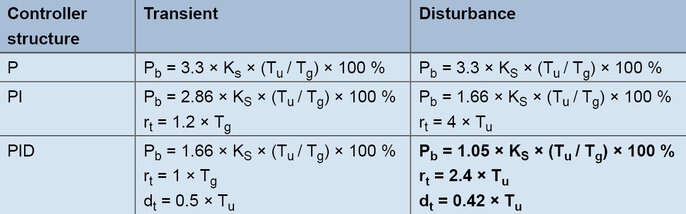
Formulas for creation according to the line step response
Example:
A controller with a PID structure is to be used for a laboratory furnace. The aim is to achieve good disturbance behavior, and the typical setpoint values are 200 °C. The output level is gradually increased in manual mode until the actual value is slightly below the future setpoint value (wait for the respective compensation processes). For example, a temperature of 180 °C is reached with an output level of 60 %. Starting from 60 %, the output level is suddenly increased to 80 % and the actual value is recorded.
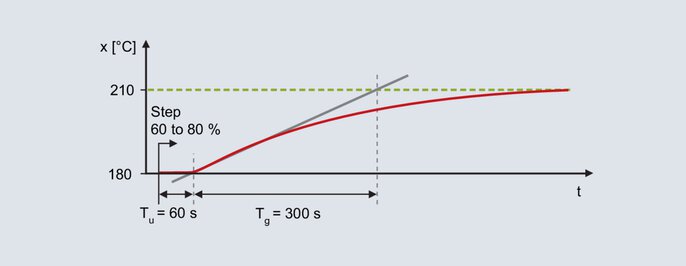
Step response of the laboratory furnace
From the step response determination takes place with the aid of the inflectional tangent: delay time Tu = 60 s, compensation time Tg = 300 s. The transmission coefficient of the control process results from the change in the actual value divided by the output step.

Equation 22
Using the rules of thumb, this results in the following parameters for the disturbance behavior:
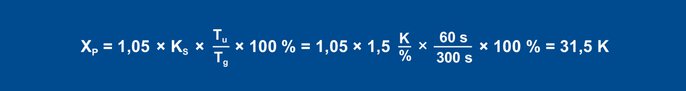
Equation 23
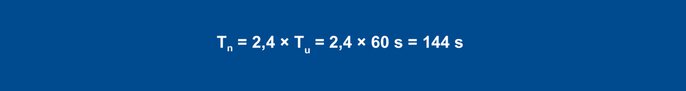
Equation 24
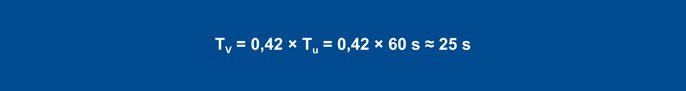
Equation 25
The output step must be performed in the area of the subsequent working point. Additionally, the step size must be set high enough to enable analysis of the course of the actual value. Once the output step has been specified, it is necessary to wait for the end value of the actual value. A time-saving alternative is the method according to the rate of rise.
Method according to the rate of rise
In terms of the step change specification, the procedure is the same as that for the method on the basis of the process step response. Prior to the step change, an output level is specified that results in an actual value that is slightly less than the setpoint value used later on.
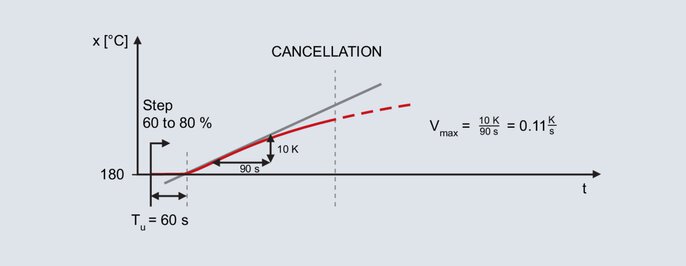
Actual value curve for the method according to slew rate
The step change is specified again for the already mentioned laboratory furnace, whereby the subsequent working point is also 200 °C. Specifying an output level of 60 % in manual mode results in an actual value of 180 °C. The output level is suddenly increased to 80 %.
After specifying the step change, the actual value increases after a while. The recording continues until the actual value reaches its maximum slope. The inflectional tangent is also drawn and the delay time determined with this method as well. The second characterizing parameter is the maximum rate of rise, which corresponds to the slope of the inflectional tangent. The maximum rate of rise can be determined by applying a slope triangle to the inflectional tangent:
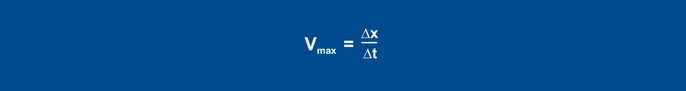
Equation 26
The calculated values Vmax (0.11 K/s) and Tu (60 s) are used in the following formulas:
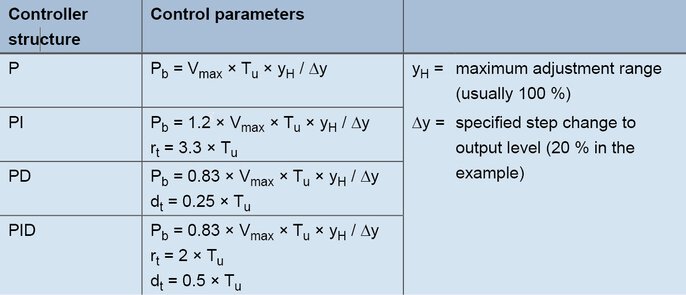
Formulas for setting according to the rate of rise
For a PID controller, the following values arise with the formulas:

Equation 27
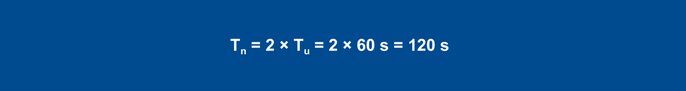
Equation 28
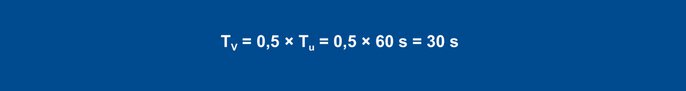
Equation 29
Empirical method for calculating control parameters
This method is used to successively calculate optimal settings for the P, D, and I components. Starting from the original state (an output level of 0 %), the typical setpoint value is specified each time; the method is therefore only suitable for relatively fast control processes (such as fast temperature control processes or control variables such as speed or flow).
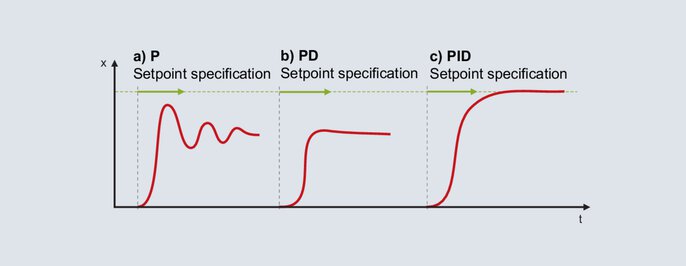
Setting of a PID controller according to the empirical method
The P structure is activated for the controller. The proportional band is set relatively large (the dimensioning depends on the control process) and the setpoint value in the subsequent working range is specified. The actual value will move slowly toward the end value and a relatively large control deviation is produced. The setpoint value is then specified with an increasingly small proportional band Pb. The aim is to achieve a Pb with which the actual value reaches its stable end value after 2 to 3 complete oscillations (Figure 56a). For a smooth start-up, the structure needs to be switched from P to PD. Starting with a small setting for the derivative time, the setpoint is specified with an increasingly large dt. If the actual value reaches its end value with as small an oscillation as possible, dt is at its optimal setting (Figure 56b).
Note: as soon as the controller sets the output level to 0 % even just once during start-up, this means that dt is set too large.
The I component is activated when the structure is switched to PID. An optimal reset time rt is generally set at 4 times the value of the previously determined dt. Figure 56c shows the response for a setting of rt = 4 × dt.
On some processes it is not possible to activate all components. If, with a P structure, an unsettled response is already produced with a large Pb, it will not be possible to use the P or the D structure. The I controller needs to be used instead.
If the P controller was successfully tuned, but the introduction of the D component makes the control loop unstable, the PI structure is used.
How can a PID controller be manually reoptimized?
Applying one of the tuning methods outlined in this chapter will most probably result in a stable, but not optimal control response. The control result can be further improved by manual retuning. If the response of a PID controller can be matched with one of the curves 62b to 62e, you will find information here for further tuning.
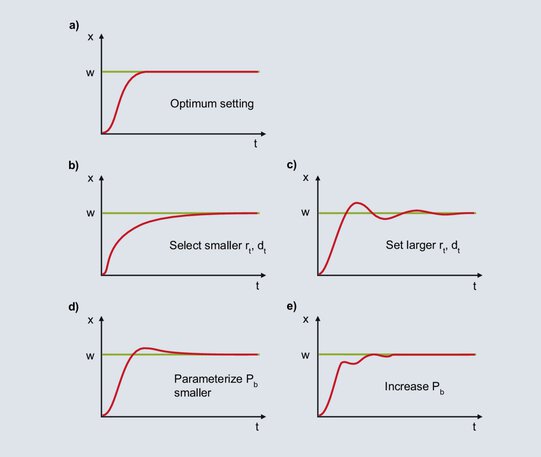
Fig. 62: Notes on the post-tuning of a PID controller
a)
The diagram shows optimal behavior for a PID controller.
b)
After specification of the setpoint value, the actual value increases steeply until it reaches the proportional band. If the actual value enters the proportional band, the P component is reduced and the I component ensures the value is adjusted to the setpoint value. The increase of the I component takes place slowly on account of the relatively large rt and the control deviation is slowly eliminated. For faster integration, rt must be set smaller; dt is also reduced in line with the ratio dt/rt = 1/4.
c)
When the actual value enters the proportional band, the I component increases the output level. The increase continues until the actual value reaches the setpoint value. In the example shown, the I component builds up an excessive output level until the elimination of the control deviation, and the actual value surpasses the setpoint value. If there is a negative control deviation, the output level is reduced too quickly and the actual value falls below the setpoint value, and so on. The symmetrical oscillation of the actual value around the setpoint value is indicative of too small an rt. rt must be increased and dt also increased in line with the ratio dt / rt = 1/4.
d)
The I component is formed from the time the actual value enters the proportional band until the elimination of the control deviation. Due to the large Pb, the I component already starts to form its output level when there is a large control deviation. Due to the large control deviation at the start, the I component forms its output level relatively quickly. When the control deviation is eliminated the I component is too large and the actual value surpasses the setpoint value. With a smaller setting for Pb, if there are smaller control deviations the I component starts to build up its output level at a correspondingly slower rate. The one-off overshoot depicted becomes more improbable.
e)
With a Pb that is set too small, the output level of the P component is reduced shortly before the setpoint value is reached. When the actual value enters the proportional band, the P component is sharply reduced and the actual value decreases. Due to the larger control deviation the output level becomes larger and the actual value increases. In the proportional band, small changes in the actual value lead to large changes in the output level, resulting in a high tendency for oscillation. This is calmed by increasing the proportional band.
- ${title}${badge}


